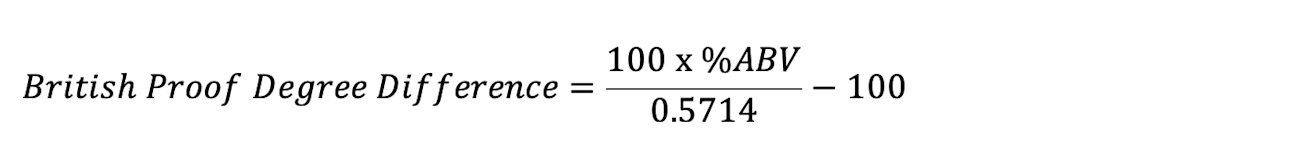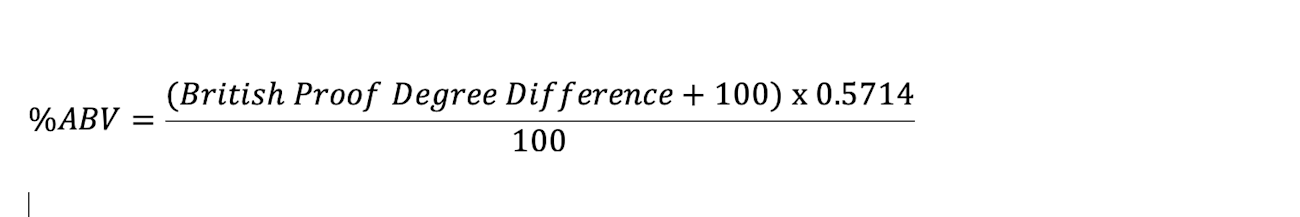Being able to measure the alcohol content of a spirit is an important skill for a distiller. If you don’t know the amount of alcohol in your products, you won’t be able to keep your products consistent, and you will undoubtedly run afoul of the tax man.
However, you may not realize that there are more ways to measure alcohol content than ABV and proof. In fact, there are so many different ways to do it, you could devote an entire book to the subject. Sadly, we don’t have that kind of space in a single article, so here are two of the most-common alternative ways to measure alcohol content in the products in the distillery.
[PAYWALL]
Mole Fraction
Mole fraction, or molar fraction as it is sometimes called, represents the ratio of a substance (N1) in moles to all the constituent parts of the substance in moles (Ntotal) (see the equation below).
Mole fractions are definitely not a common unit in which to report alcohol. Actually, outside of a chemical supplier to laboratories, you’d be hard pressed to find a merchant who sells alcohol in mole fractions. Nevertheless, knowing what mole fractions are, and how to report alcohol content in them, is an important skill for distillers because they’re the preferred unit of chemical engineers when designing distillation systems. That makes it vitally important that you can convert between standard alcohol contents and mole fractions.
Calculating the mole fraction of a substance is relatively straightforward, although it does take a bit of math. The first thing you need to find is the number of moles of the subject constituent in a solution. A mole is a unit in chemistry that is equal to 6.022147067 x 1023, and it’s usually used to measure things such as atoms or molecules.
To calculate the number of moles of a molecule, such as ethanol, you need to look up the molecule’s molecular mass, then divide the weight of that molecule in the substance by the molecular mass. That will give the exact number of molecules of that constituent in moles. Once you’ve found the number of moles of the subject constituent, you need to calculate the total number of moles of all other constituents. Then you divide the moles of the subject constituent by the number of moles of all constituents to get the mole fraction.
Hey, I said it was straightforward! I didn’t say it was easy. Perhaps an example will make things a little clearer.
Let’s say we have 1,000 grams of a 50 percent water-and-ethanol solution, by weight, and we want to determine the mole fraction of ethanol. (I know I just used ABW, which is another method for measuring alcohol content. That method will get its own write up ... eventually).
The first thing we need to do is find the moles of ethanol. Upon looking up the molecular mass of ethanol (thank you, Google), we find that it is equal to 46.068 grams/mol. (Note: there is a way to calculate this by adding the molecular weight of each of the atoms, but that’s beyond the scope of this article.) Because we know that 50 percent of the weight of the solution is ethanol and 50 percent of 1,000 grams is 500 grams, we know that we have 500 grams of pure ethanol available in solution and 500 grams of water. That 500 grams of ethanol divided by 46.068 g/mol gives us a total of 10.853 moles of ethanol.
Now we need to calculate the number of moles of water. We look it up and find that one mole of water is equal to 18.015 grams/mol. Because we already know that we have 500 grams of water, we divide that by 18.015 grams/mol to find that there are 27.755 moles of water in the solution. From there, we simply divide the number of moles of ethanol, 10.853 moles, by the number of moles of ethanol plus water, 10.853 moles + 27.755 moles. This gives us a mole fraction of 0.281 or 28.1 percent mole fraction ethanol. For a clearer understanding, see the equations below.
Chemical engineers use mole fractions to create mass balance equations for continuous columns, and they play an important role in the Fenske equation, which is used to calculate the number of theoretical plates required to achieve a desired alcohol content.
Knowing the mole fractional ethanol content of your distillery’s inputs and desired outputs is incredibly important when communicating with engineers because it allows each party to speak the same language. If you can’t calculate mole fractions when talking to your engineer, there is a very real chance that key parts of your process may be improperly designed.
British Proof
For distillers in the United States, the use of the term “proof” is common. Indeed, on its operational reports, the TTB still requires that all spirits production be reported in proof gallons, and most U.S. liquor store shelves are awash with bottles reporting their alcohol content as proof rather than ABV. However, it may surprise some to know that the modern day TTB definition of proof—equal to two times the ABV—is not the original definition.
The British government first introduced the initial proof system in the late 1700s, concurrent with the invention and widespread acceptance of hydrometry. Early hydrometers were crude by today’s standards, and they built their definition of proof from the even earlier and cruder “gunpowder test,” which determined alcohol as either being above or below proof based on how well it burned when mixed with gunpowder. That basis led to the establishment of 57.14 percent ABV as the standard of at-proof alcohol—or equal to either 0 proof or 100 proof, depending on what form of the system you were using. Alcohol produced using this early system was reported in relation to 57.14 percent ABV in terms of degrees overproof or underproof; with the maximum value of 75 degrees overproof (175 proof) equaling 100 percent pure alcohol. Confusing, I know.
To make matters worse, some distillers also liked to report their alcohol in fractions with a base of seven, with four-sevenths (4/7) being roughly equal to at-proof alcohol (again, 57.14 percent ABV). This is why it’s common to see many older bottles of spirit with the term “4/7ths proof” stamped somewhere on the label followed by a proof number and ABV that make no sense to users of today’s ABV and proof system.
Converting between modern-day ABV and British proof is not terribly difficult, but it does require several steps. The first step is to convert the ABV into proof degrees, using the formula below. If the proof degrees difference is positive, the product can be stated in degrees overproof; if it is negative, it is stated as degrees underproof.
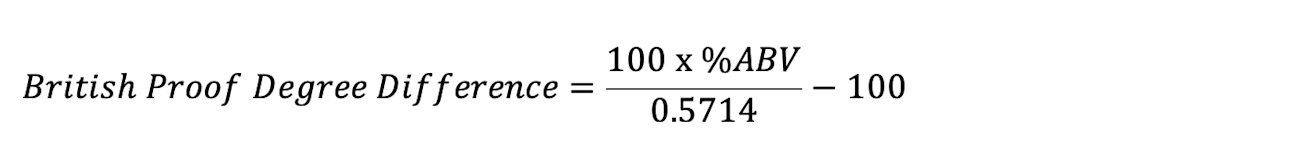
The best way to really understand the British proofing system is to see it in action. Below are two real-world examples for both an overproof and underproof product.
Example 1: Overproof
We have a rum that is measured at 70 percent ABV. So, 70 percent ABV times 100, divided by 0.5714 is equal to 122; 122 minus 100 equals +22 degrees of difference. Therefore, the rum can be said to be 22 degrees overproof.
Example 2: Underproof
We have gin that is measured at 43 percent ABV. So, 43 percent ABV times 100, divided by 0.5714 is equal to 75.25 proof. Then, 75.25 proof minus 100 equals -24.75 degrees of difference. Therefore, the gin can be said to be 24.75 degrees underproof.
To convert from British Proof to ABV is a simple matter of reversing the previous equation so that it solves for ABV instead of proof:
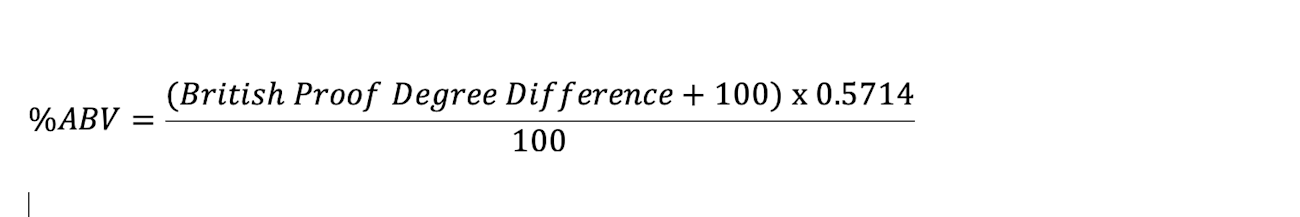
A good real-world example of this equation in action can be seen below.
Example 3: British Proof to ABV
We have a whiskey at 10 degrees underproof: -10 plus 100, times 0.5714 is equal to 51.426. 51.426 divided by 100 is equal to 51.43 percent. Thus, the whiskey is 51.43 percent ABV.
Mercifully, the U.K. government eventually abandoned its use of the British proof system in 1980 in favor of the now-standard, and simpler, European OIML (International Organization of Legal Metrology) method for measuring alcohol. That said, many producers around the world still use the old proofing system to name and promote their products. This is especially true in the rum and gin worlds, where the popularity of overproof and navy-strength products remains a major selling point. There has also been an explosion in trading of old bottles recently, all of which are still labeled with the old proofing system. For these reasons, it’s important that distillers know and can convert between the old and new system with ease.
Note: Some sources state that colonial governments, most notably the Canadian government, used 57.06 percent ABV as their basis for 100-proof. This is entirely probable. Before the establishment of international measuring conventions, there was a large amount of variability among government standards. Regardless, the difference in results between 57.14 percent ABV and 57.06 percent ABV is minimal, and these two numbers should be able to be used interchangeably as long as they are not being used for government reporting.
Mole fractions and British proof are just two of the dozens, if not hundreds, of methods for measuring alcohol content in a substance. True, they may not be the most-common methods; however, they still have their place. As a distiller, you should at least be familiar with some of the less-common methods for measuring alcohol content. That way you don’t ever find yourself lost in translation when speaking to someone new.
