Statistics, But Not Damned Lies: Analyzing Your Spirits

Setting up a serious sensory program at your distillery is a key step to ensuring the quality of your spirits. Previously, we examined how to recruit evaluators and properly run a sensory session. Here, we look at how sensory scientists analyze the results.

First, however, we need to review a little about statistics, so we can better understand how to use them as a tool in the service of quality.

[PAYWALL]

Why Statistics Matter

There are many different types of tests that sensory scientists use, and each test results in varying types of data. To interpret these data and turn them into actionable information, sensory scientists must use statistics.

Statistics is a complex and far-reaching field of mathematics, and many people have devoted their entire lives to understanding and improving that field. Luckily, thanks to advancements in technology, sensory scientists can use computers or pre-existing models for many of the tests. However, it’s still important for anyone working in sensory analysis to be familiar with some basic concepts and tools—namely, bell curves and the null hypothesis.

Bell Curves

In statistics, there are two major branches of analysis: parametric and non-parametric. Non-parametric statistics—those that minimize assumptions, such as whether data will fit a distribution type—are not typically used in sensory science, so we will focus instead on parametric statistics.

Parametric statistics are based on the analysis of data sets that are assumed to adhere to Gaussian distribution. Gaussian data sets form a bell curve—that is, the most likely outcomes are grouped in the center, with the least likely toward the edges. By using this curve, statisticians can calculate a mean and standard deviation for specific results, and then they can predict the likelihood that this result happened at random or whether there is another factor influencing the result. This sounds complicated, but it’s actually very simple.

For example: If we were conducting a discriminative test in which all of the samples are the same, we would expect evaluators to choose samples at random. This should result in each sample being chosen an equal number of times, giving us a normal distribution of data that would fit toward the center of a bell curve. However, perhaps there is an unknown difference among the samples, and that difference pushes evaluators to choose one sample more often. That difference will result in a data set that does not fit well underneath the standard expected bell curve.

Sensory scientists can then use this information to determine whether some unaccounted-for factor is affecting the results of the test.

The Null Hypothesis and Confidence

When conducting difference testing, sensory scientists are concerned with either accepting or rejecting what is known as the null hypothesis.

Simply put, the null hypothesis is the hypothesis that there is no difference among any of the samples tested. If sensory scientists accept the null hypothesis, then they have concluded that the samples are the same; if they reject the null hypothesis, they have concluded that the samples are different.

There are two types of error that can occur when accepting or rejecting a null hypothesis. The first type, known as a Type I error, occurs if we reject the null hypothesis when it is true. This means that we would determine there is a difference among samples when there is actually not. The second type of error, Type II, occurs if we accept the null hypothesis when there is actually a difference among the samples. The chances of Type I and Type II error occurring are represented by the Greek symbols ⍺ (alpha) and β (beta), respectively.

Before sensory scientists can accept or reject a null hypothesis, they must determine how much chance of Type I and Type II error they are willing to accept. This is known as determining the confidence level of a result. Knowing a test’s required minimum confidence level will help to define the number of evaluators needed to conduct a test. This is especially important in experimental design.

Traditionally, most sensory tests operate with an ⍺ and β risk of either 0.05 or 0.01; that translates to a 95 percent or 99 percent confidence level. In the case of very large tests with lots of participants, sensory scientists can sometimes reach a confidence level of 99.9 percent—however, no matter how many evaluators you have, it is impossible to reach a confidence level of 100 percent. There will always be a chance that an error has occurred.

Applying Statistical Principles

Now that we know a little of what statistics can do, we need to understand why they are important to sensory analysis.

Every sensory test—be it descriptive, discriminative, or hedonic—has its own statistical rules that it must follow for the results to be valid. The job of a sensory scientist is to pick the right test and statistical approach for each situation. Although this seems easy, it can sometimes be difficult.

For example, triangle testing is one of the most popular sensory tests within the beverage world. However, in certain situations, it requires far too many evaluators to participate for its results to be statistically valid. This is especially true when trying to test for similarity. Furthermore, although triangle tests are great at determining difference, they do nothing to determine the scale of that difference, which sometimes may be more important information.

It’s essential that a successful sensory scientist consider the statistical and operational advantages and disadvantages of each test. Just because a test seems easy to conduct doesn’t necessarily mean that it will give you statistically relevant results. Test methods and analysis have to work in synergy to answer the stated goal of the experiment.

This can all be complicated. So, here is a quick example that should help to make things a little clearer.

A Real-World Example

XYZ Distilling Company has been producing their award-winning XYZ Bourbon for the past five years using a locally sourced variety of corn. Unfortunately, because of a bad harvest this year, the farm that normally supplies all the corn is unable to fulfill its grain orders for the year. However, there is another farm that grows a similar variety of corn that can bridge the gap—but there is some concern that the flavor of the distillate will be changed.

To properly assess whether this new variety of corn will significantly change the distillate, XYZ’s distiller decides to do discrimination testing on distillate made with both varieties.

After some consideration, the distiller determines that because of the importance of this test, the results must have at least 95 percent confidence before he considers rejecting the null hypothesis. Normally, for difference testing, XYZ Distillery prefers to use triangle testing—but because this test has to be done last-minute, there are only a limited number of assessors available.

After consulting some reference materials on available tests, the distiller decides that tetrad testing is the best possible discriminative test to use because tetrad testing, which involves pairing four samples into two like groups, is considered more statistically powerful than many other discrimination tests when testing in small groups. Thus, any results will likely be able to meet the required confidence level to be accepted or rejected.

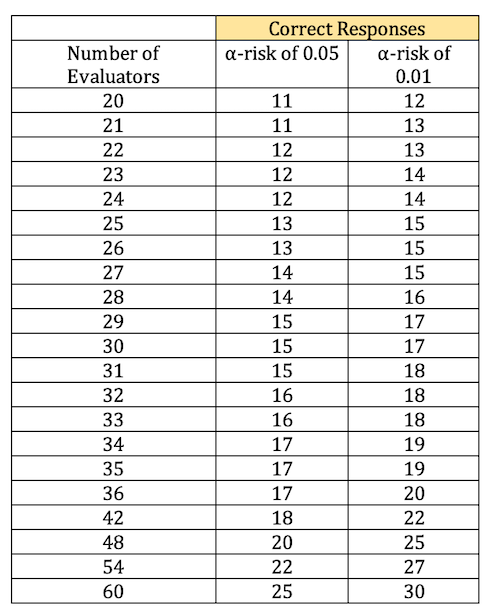
Upon completion of the test, the distiller determines that 16 of the 35 participants were able to accurately pair the two samples together. Unfortunately, during the test, two of the evaluators appeared to be experiencing severe sensory fatigue—one of those submitted an accurate answer, and the other an inaccurate one.

Using the table below, the distiller is able to determine that not enough people were able to correctly differentiate between the two distillates to reject the null hypothesis. This is true whether or not the two sensory-fatigued individuals’ responses are included. That means that XYZ Distilling is able to comfortably use the new variety of corn because it does not seem to create a noticeable difference in the distillate.

This table gives the required number of correct responses in a tetrad test for a null hypothesis to be rejected with varying levels of confidence:

Other Testing Methods

For simplicity’s sake, I’ve been focusing here mainly on discriminative testing and basic statistics because these methods are by far the most common in the beverage industry. However, there are two other statistical methods of note that are sometimes used in sensory science. The first is analysis of variance, often shortened to ANOVA. ANOVA is a way of analyzing multivariate data, and it’s mostly used in descriptive testing to help relate sensory attributes to each other.

The second statistical method is called principal component analysis (PCA). PCA is a highly complicated statistical method that creates a 3D model of how samples relate to each other. This can especially be helpful when creating new products or assessing products in comparison to others on the market.

Both methods require extensive training and complicated computer modeling to be used correctly; in the right hands, however, they can be powerful tools.